Key Assumptions of the Dependent T-Test Explained What Are the Assumptions of the Dependent T-Test? Dependent T-Test Assumptions: A Quick Guide Understanding Assumptions for the Dependent T-Test Essential Assumptions of the Dependent T-Test

The dependent t-test, also known as the paired t-test, is a statistical method used to compare the means of two related groups. It’s a powerful tool for analyzing before-and-after scenarios or matched pairs. However, like any statistical test, it relies on specific assumptions to ensure accurate results. Understanding these assumptions is crucial for anyone conducting research or analyzing data. Below, we break down the key assumptions of the dependent t-test and explain why they matter.
What Are the Assumptions of the Dependent T-Test?

The dependent t-test rests on several critical assumptions. These ensure the validity and reliability of your results. Let’s explore them in detail.
1. Paired or Dependent Samples
The first assumption is that the samples being compared are dependent or paired. This means the observations in one group are directly related to those in the other group. Common examples include pre-test and post-test scores or measurements from matched subjects.
📌 Note: Ensure your data is truly paired; otherwise, consider using an independent t-test instead.
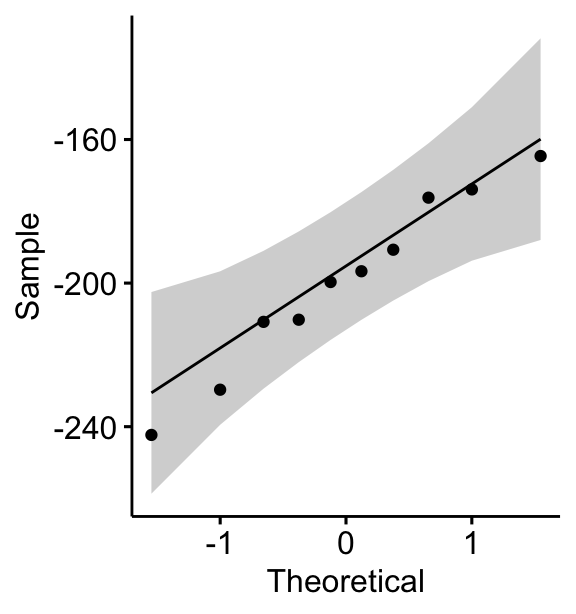
2. Normality of Differences
The differences between the paired observations must follow a normal distribution. This assumption is crucial because the t-test relies on the properties of the normal distribution to calculate p-values and confidence intervals.
- How to Check: Use visual methods like Q-Q plots or statistical tests like Shapiro-Wilk.
- Small Sample Exception: For small samples (n < 30), the Central Limit Theorem often allows for minor deviations from normality.
3. Random Sampling
The data should be collected through random sampling to ensure the results are generalizable to the population. Non-random samples can introduce bias, compromising the validity of the test.
4. Absence of Outliers
Outliers can significantly distort the results of a dependent t-test. It’s essential to identify and address outliers before proceeding with the analysis.
- Detection: Use box plots or z-scores.
- Handling: Consider removing outliers or transforming the data if they are not influential.
Dependent T-Test Assumptions: A Quick Guide

To summarize, the essential assumptions of the dependent t-test are:
1. Paired or dependent samples.
2. Normality of differences.
3. Random sampling.
4. Absence of outliers.
| Assumption | Importance | How to Verify |
|---|---|---|
| Paired Samples | Ensures the test is appropriate | Check data structure |
| Normality of Differences | Validates t-test results | Q-Q plots, Shapiro-Wilk test |
| Random Sampling | Ensures generalizability | Review data collection method |
| No Outliers | Prevents distortion of results | Box plots, z-scores |

Understanding Assumptions for the Dependent T-Test

Violating these assumptions can lead to incorrect conclusions. For instance, non-normal data may inflate Type I errors, while outliers can skew the mean differences. Always verify assumptions before interpreting your results.
📌 Note: If assumptions are violated, consider non-parametric alternatives like the Wilcoxon signed-rank test.
Essential Assumptions of the Dependent T-Test: Checklist
Before running a dependent t-test, use this checklist to ensure your data meets the assumptions:
- [ ] Confirm data is paired or dependent.
- [ ] Check normality of differences.
- [ ] Verify random sampling.
- [ ] Identify and address outliers.
By adhering to these assumptions, you’ll ensure the reliability and accuracy of your dependent t-test results.
What is the dependent t-test used for?
+The dependent t-test is used to compare the means of two related groups, such as pre-test and post-test scores or matched pairs.
What happens if the normality assumption is violated?
+Violating the normality assumption can lead to inaccurate p-values and conclusions. Consider non-parametric tests or data transformations.
Can I use the dependent t-test for independent samples?
+No, the dependent t-test is specifically for paired or related samples. Use the independent t-test for unrelated groups.
In summary, the dependent t-test is a valuable tool for comparing related groups, but its assumptions must be carefully checked. By ensuring paired samples, normality of differences, random sampling, and the absence of outliers, you’ll produce robust and reliable results. Always verify these assumptions before drawing conclusions, and consider alternatives if they’re violated.
dependent t-test assumptions, paired t-test requirements, statistical test assumptions

