Cartesian to Spherical Conversion Made Easy

Converting Cartesian coordinates to spherical coordinates is a fundamental skill in mathematics, physics, and engineering. Whether you're working on 3D modeling, analyzing spatial data, or solving complex equations, understanding this conversion is crucial. In this guide, we’ll break down the process step-by-step, making it easy for both beginners and professionals. By the end, you’ll master Cartesian to spherical conversion and apply it confidently in your projects. (coordinate systems,3D modeling,spatial data)
Understanding Cartesian and Spherical Coordinates
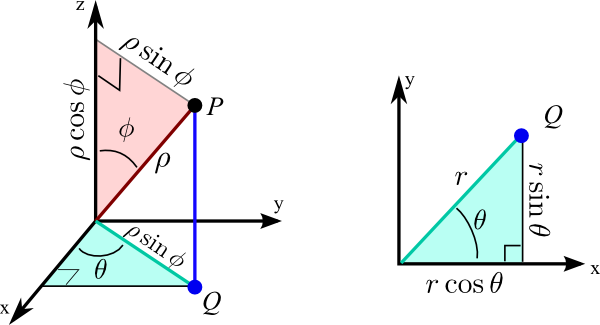
Before diving into the conversion, let’s clarify what these coordinate systems represent. Cartesian coordinates (x, y, z) describe a point in 3D space using perpendicular axes. Spherical coordinates (ρ, θ, φ), on the other hand, use a radius (ρ), polar angle (θ), and azimuth angle (φ) to locate a point. This system is ideal for scenarios involving radial symmetry or spherical shapes. (3D space,radial symmetry,azimuth angle)
The Cartesian to Spherical Conversion Formula

The conversion involves three key formulas:
1. Radius (ρ): ρ = √(x² + y² + z²)
2. Polar Angle (θ): θ = arccos(z / ρ)
3. Azimuth Angle (φ): φ = arctan(y / x)
These equations transform Cartesian (x, y, z) into spherical (ρ, θ, φ) coordinates seamlessly. (conversion formula,polar angle,azimuth angle)
📌 Note: Ensure your calculator is set to radians for accurate angle calculations.
Step-by-Step Conversion Process

Step 1: Calculate the Radius (ρ)
Start by finding the distance from the origin to the point using the formula for ρ. This lays the foundation for further calculations. (distance calculation,origin point)
Step 2: Determine the Polar Angle (θ)
Use the z-coordinate and ρ to find θ. This angle measures the deviation from the positive z-axis. (polar angle,z-axis)
Step 3: Find the Azimuth Angle (φ)
Calculate φ using the x and y coordinates. This angle represents the rotation in the xy-plane. (azimuth angle,xy-plane)
Practical Applications of Spherical Coordinates

Spherical coordinates are widely used in:
- Physics: Describing gravitational fields or wave functions.
- Engineering: Modeling spherical structures or antenna patterns.
- Graphics: Rendering 3D scenes with radial symmetry.
Mastering this conversion unlocks new possibilities in these fields. (gravitational fields,3D rendering,antenna patterns)
Checklist for Cartesian to Spherical Conversion

- Verify Cartesian coordinates (x, y, z) are correct.
- Calculate ρ using the distance formula.
- Determine θ with the arccos function.
- Find φ using the arctan function.
- Double-check units (radians vs. degrees).
By following this guide, you’ve simplified Cartesian to spherical conversion and gained a valuable skill for technical applications. Practice with different coordinate sets to reinforce your understanding. (coordinate conversion,technical applications,practice exercises)
What are Cartesian coordinates used for?
+
Cartesian coordinates are used to represent points in 2D or 3D space using perpendicular axes (x, y, z). They’re common in geometry, physics, and computer graphics. (geometry,computer graphics,3D space)
Why use spherical coordinates instead of Cartesian?
+
Spherical coordinates simplify problems with radial symmetry or spherical shapes, making calculations more efficient in certain scenarios. (radial symmetry,spherical shapes,efficiency)
How do I handle negative coordinates in conversion?
+
Negative coordinates affect the azimuth angle (φ). Use the arctan2 function to account for the correct quadrant. (azimuth angle,arctan2 function,quadrant)


