How to Find the Derivative of 1/(1+x) Easily

Finding the derivative of \frac{1}{1+x} can seem daunting at first, but with the right approach, it becomes straightforward. This function is a classic example of a rational function, and its derivative can be found using the quotient rule or a simpler method involving algebraic manipulation. Whether you're a student tackling calculus for the first time or a professional refreshing your skills, this guide will walk you through the process step-by-step, ensuring you understand the logic behind each step. (derivative of 1/(1+x), calculus tutorial, rational function)

Understanding the Function ( \frac{1}{1+x} )

Before diving into the derivative, let’s understand the function itself. ( \frac{1}{1+x} ) is a rational function where the numerator is a constant (1), and the denominator is a linear expression ((1+x)). This function is well-behaved and differentiable for all ( x \neq -1 ). (rational function, differentiability)

Why Use Algebraic Manipulation?

While the quotient rule is a standard method for differentiating rational functions, algebraic manipulation offers a simpler alternative for ( \frac{1}{1+x} ). By rewriting the function, we can apply the chain rule directly, making the process more intuitive. (algebraic manipulation, chain rule)

Step-by-Step Guide to Finding the Derivative

Let’s break down the process into manageable steps:

Step 1: Rewrite the Function

Start by expressing ( \frac{1}{1+x} ) in a form that’s easier to differentiate. Notice that:
[
\frac{1}{1+x} = (1+x)^{-1}
]
This rewrite allows us to apply the chain rule directly. (chain rule, function rewrite)

Step 2: Apply the Chain Rule

The chain rule states that if ( y = f(g(x)) ), then ( y’ = f’(g(x)) \cdot g’(x) ). Here, ( f(u) = u^{-1} ) and ( g(x) = 1+x ). Thus:
[
\frac{d}{dx}[(1+x)^{-1}] = -1 \cdot (1+x)^{-2} \cdot \frac{d}{dx}[1+x]
]
Since ( \frac{d}{dx}[1+x] = 1 ), the derivative simplifies to:
[
\frac{d}{dx}\left[\frac{1}{1+x}\right] = -\frac{1}{(1+x)^2}
]
(chain rule application, derivative simplification)

📌 Note: Always ensure the denominator is not zero when differentiating rational functions.

Summary and Checklist

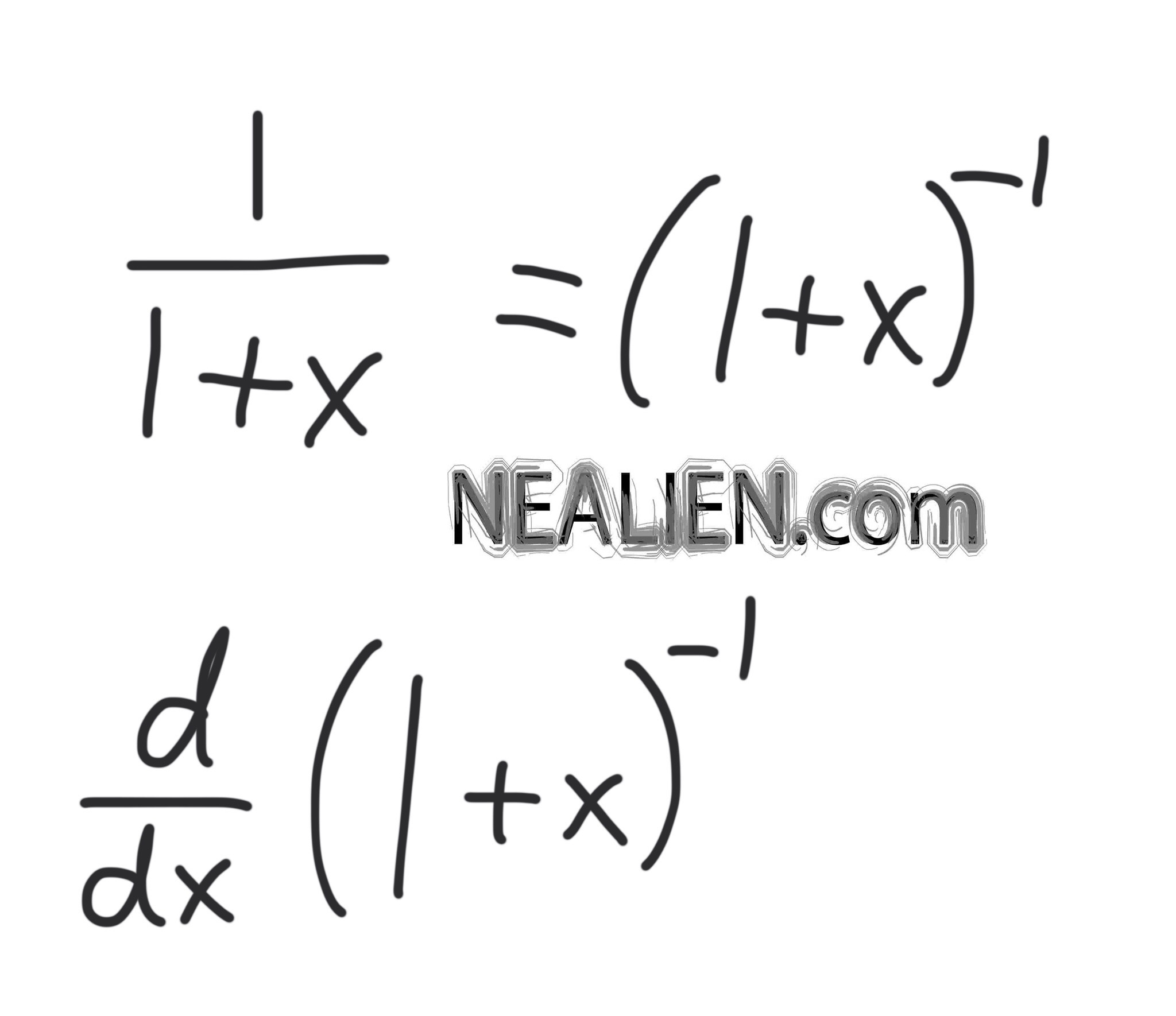
To summarize, finding the derivative of ( \frac{1}{1+x} ) involves rewriting the function and applying the chain rule. Here’s a quick checklist to guide you:

• Rewrite ( \frac{1}{1+x} ) as ( (1+x)^{-1} ).


• Apply the chain rule: ( \frac{d}{dx}[(1+x)^{-1}] = -1 \cdot (1+x)^{-2} \cdot 1 ).


• Simplify to get ( -\frac{1}{(1+x)^2} ).

By following these steps, you’ve successfully found the derivative of \frac{1}{1+x} . This method not only simplifies the process but also reinforces your understanding of calculus fundamentals. Practice this technique with similar functions to build confidence in your differentiation skills. (calculus fundamentals, differentiation practice)