Gibbs-Duhem Equation: A Key to Thermodynamic Insights

<!DOCTYPE html>
The Gibbs-Duhem equation is a fundamental relationship in thermodynamics that connects the chemical potentials of components in a system with changes in temperature, pressure, and composition. It serves as a bridge between the macroscopic and microscopic worlds, offering deep insights into the behavior of mixtures and pure substances alike. Whether you're a student, researcher, or industry professional, understanding this equation can unlock a wealth of knowledge in fields like chemistry, physics, and materials science. (Thermodynamic Principles, Chemical Engineering, Material Science)
What is the Gibbs-Duhem Equation?
The Gibbs-Duhem equation is expressed as:
Nidμi = -SdT + VdP
Where:
- Ni = Number of moles of component i
- μi = Chemical potential of component i
- S = Entropy of the system
- T = Temperature
- V = Volume of the system
- P = Pressure
This equation highlights the interdependence of thermodynamic variables, making it a powerful tool for analyzing systems under various conditions. (Thermodynamic Equations, Chemical Potentials, Phase Equilibria)
Applications of the Gibbs-Duhem Equation
Phase Equilibria and Critical Points
One of the most significant applications of the Gibbs-Duhem equation is in determining phase equilibria. By analyzing how chemical potentials change with temperature and pressure, researchers can predict phase transitions and critical points in mixtures. This is crucial in industries like petroleum refining and pharmaceutical manufacturing. (Phase Diagrams, Critical Phenomena, Industrial Applications)
Material Science and Engineering
In material science, the Gibbs-Duhem equation aids in understanding the behavior of alloys and composites. It helps engineers design materials with specific properties by predicting how changes in composition affect thermodynamic stability. (Alloy Design, Composite Materials, Thermodynamic Stability)
How to Use the Gibbs-Duhem Equation in Practice

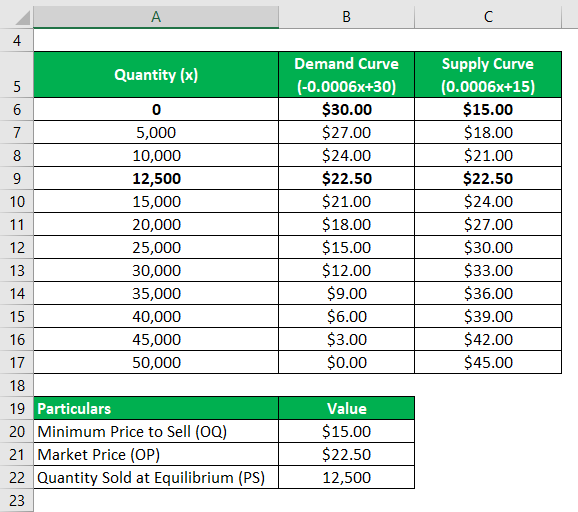
Step 1: Define Your System
Identify the components and phases in your system. This includes specifying the number of moles, temperature, pressure, and volume. (System Analysis, Thermodynamic Systems)
Step 2: Calculate Chemical Potentials
Use experimental data or theoretical models to determine the chemical potentials of each component. This step is critical for applying the Gibbs-Duhem equation effectively. (Experimental Data, Theoretical Models)
Step 3: Analyze Thermodynamic Changes
Apply the Gibbs-Duhem equation to analyze how changes in temperature, pressure, or composition affect the system. This can provide insights into phase transitions, reaction pathways, and material properties. (Thermodynamic Analysis, Phase Transitions)
📌 Note: Always ensure consistency in units when applying the Gibbs-Duhem equation to avoid errors in calculations.
Summary and Checklist

To summarize, the Gibbs-Duhem equation is a cornerstone of thermodynamics, offering critical insights into the behavior of systems under various conditions. Here’s a checklist to guide your application:
- Define the system components and phases.
- Calculate chemical potentials using reliable data or models.
- Apply the Gibbs-Duhem equation to analyze thermodynamic changes.
- Interpret results in the context of phase equilibria, material properties, or reaction pathways.
By mastering this equation, you can enhance your understanding of complex thermodynamic systems and drive innovation in your field. (Thermodynamic Insights, Innovation in Science)
What is the Gibbs-Duhem equation used for?
+The Gibbs-Duhem equation is used to relate the chemical potentials of components in a system to changes in temperature, pressure, and composition. It’s essential for understanding phase equilibria, material properties, and thermodynamic stability. (Thermodynamic Applications, Phase Equilibria)
How does the Gibbs-Duhem equation differ from other thermodynamic equations?
+Unlike equations like the ideal gas law or van der Waals equation, the Gibbs-Duhem equation focuses on the relationship between chemical potentials and thermodynamic variables, making it uniquely suited for analyzing mixtures and phase transitions. (Thermodynamic Equations, Chemical Potentials)
Can the Gibbs-Duhem equation be applied to non-ideal systems?
+Yes, the Gibbs-Duhem equation is applicable to both ideal and non-ideal systems. It provides a general framework for understanding thermodynamic behavior, regardless of the system’s complexity. (Non-Ideal Systems, Thermodynamic Behavior)