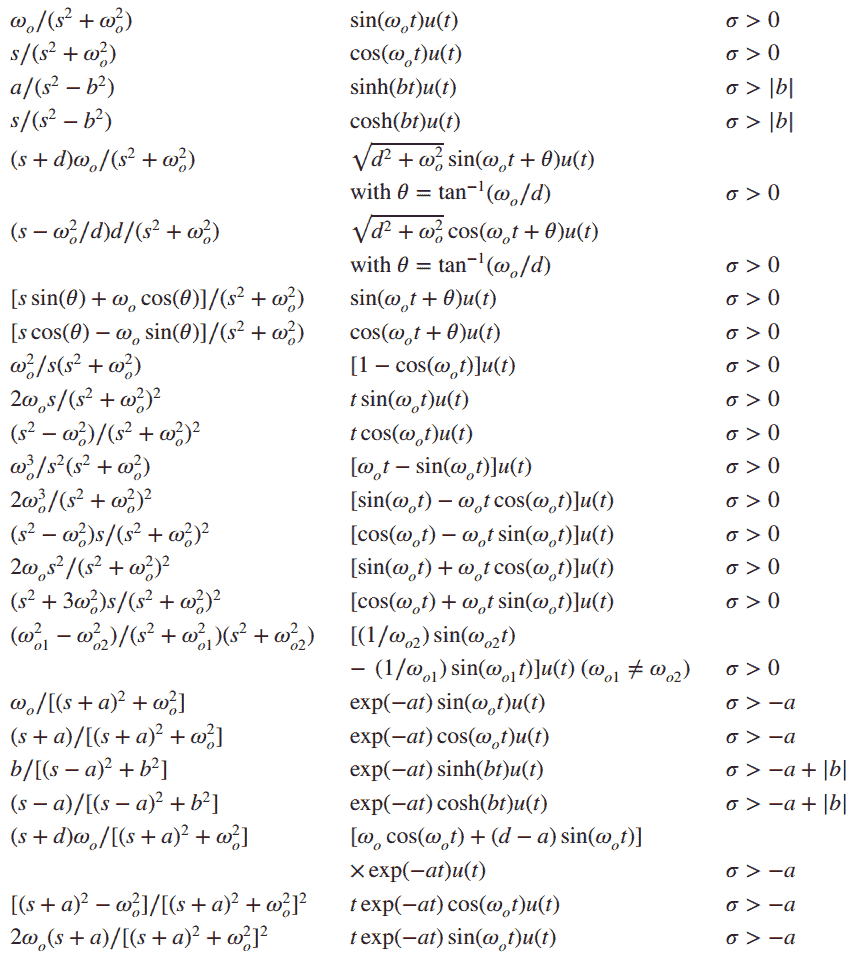
Are you struggling with complex mathematical functions and looking for a way to simplify them instantly? An Inverse Laplace Transform Calculator can be your ultimate solution. Whether you’re a student, engineer, or researcher, this tool can save you time and reduce errors in your calculations. In this post, we’ll explore how an Inverse Laplace Transform Calculator works, its benefits, and how to use it effectively.
What is an Inverse Laplace Transform Calculator?
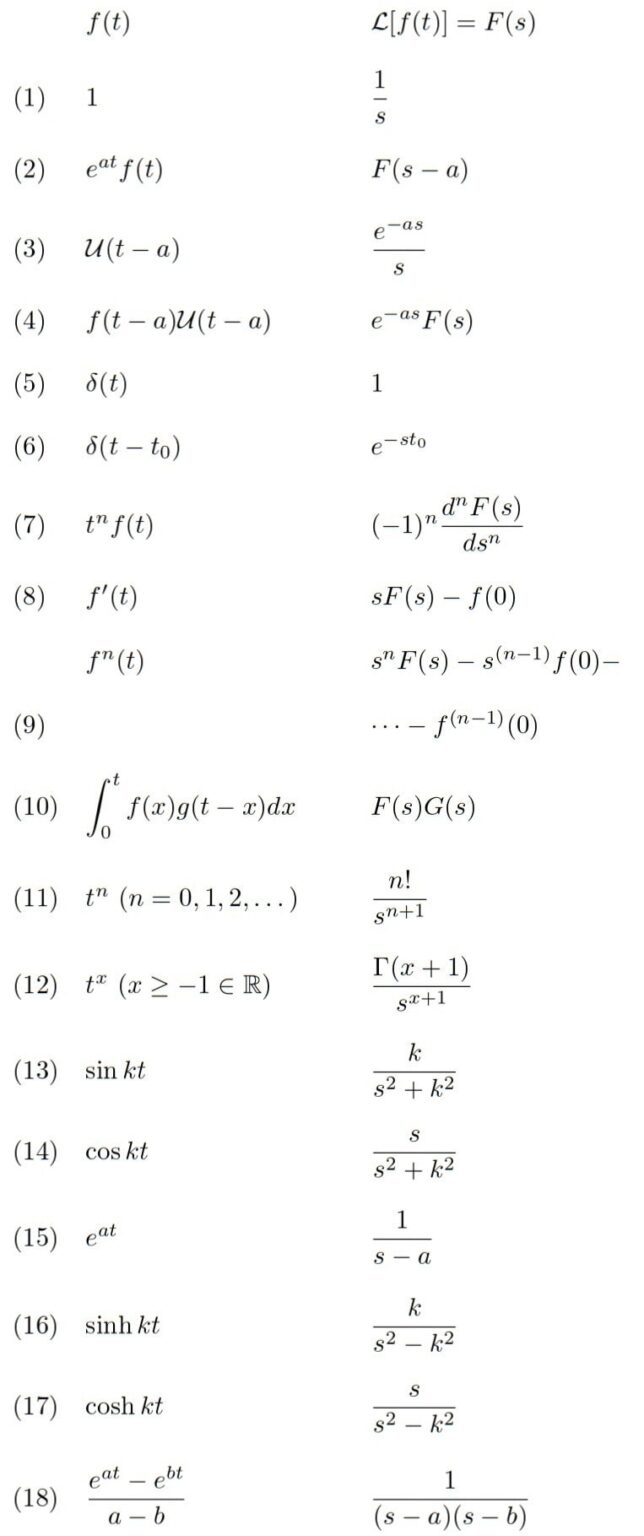
An Inverse Laplace Transform Calculator is a powerful tool designed to convert Laplace domain functions back into the time domain. This process is essential in solving differential equations, control systems, and signal processing problems. By automating the transformation, the calculator eliminates the need for manual computations, which can be time-consuming and prone to mistakes.
💡 Note: The Inverse Laplace Transform is the reverse process of the Laplace Transform, making it crucial for analyzing dynamic systems.
Why Use an Inverse Laplace Transform Calculator?
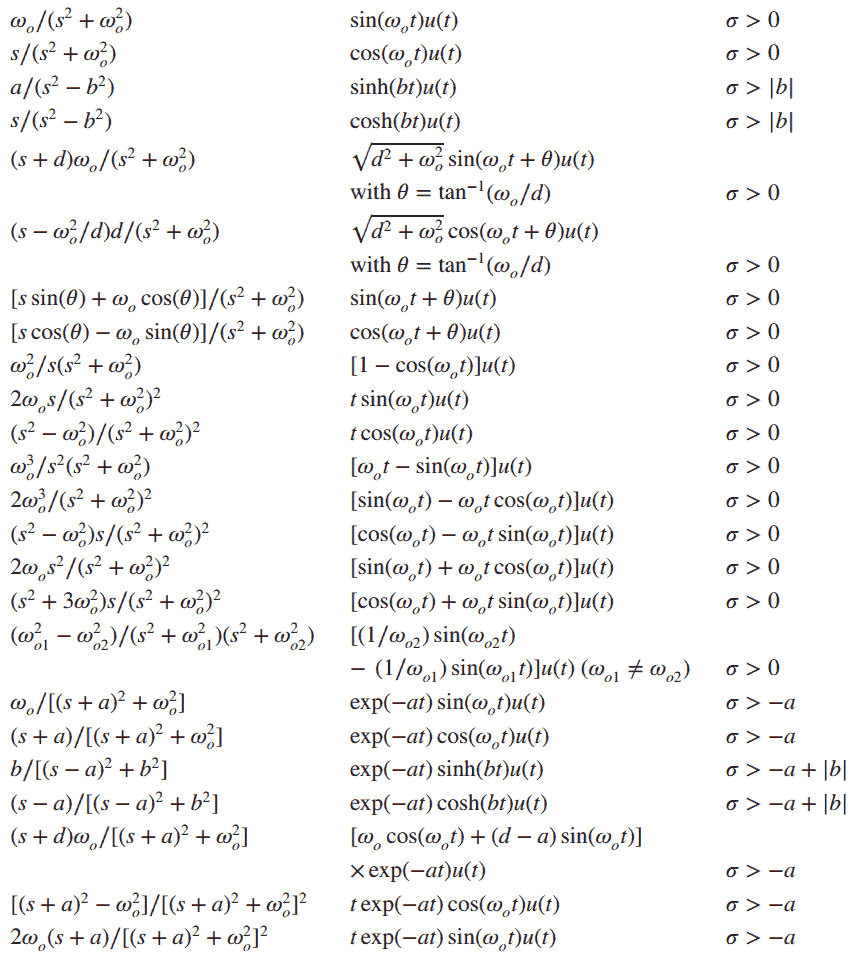
Using an Inverse Laplace Transform Calculator offers several advantages:
- Time Efficiency: Quickly solve complex functions without manual calculations.
- Accuracy: Reduce errors that often occur in manual transformations.
- Accessibility: Available online, making it easy to use anytime, anywhere.
- Versatility: Applicable in various fields like engineering, physics, and mathematics.
How to Use an Inverse Laplace Transform Calculator
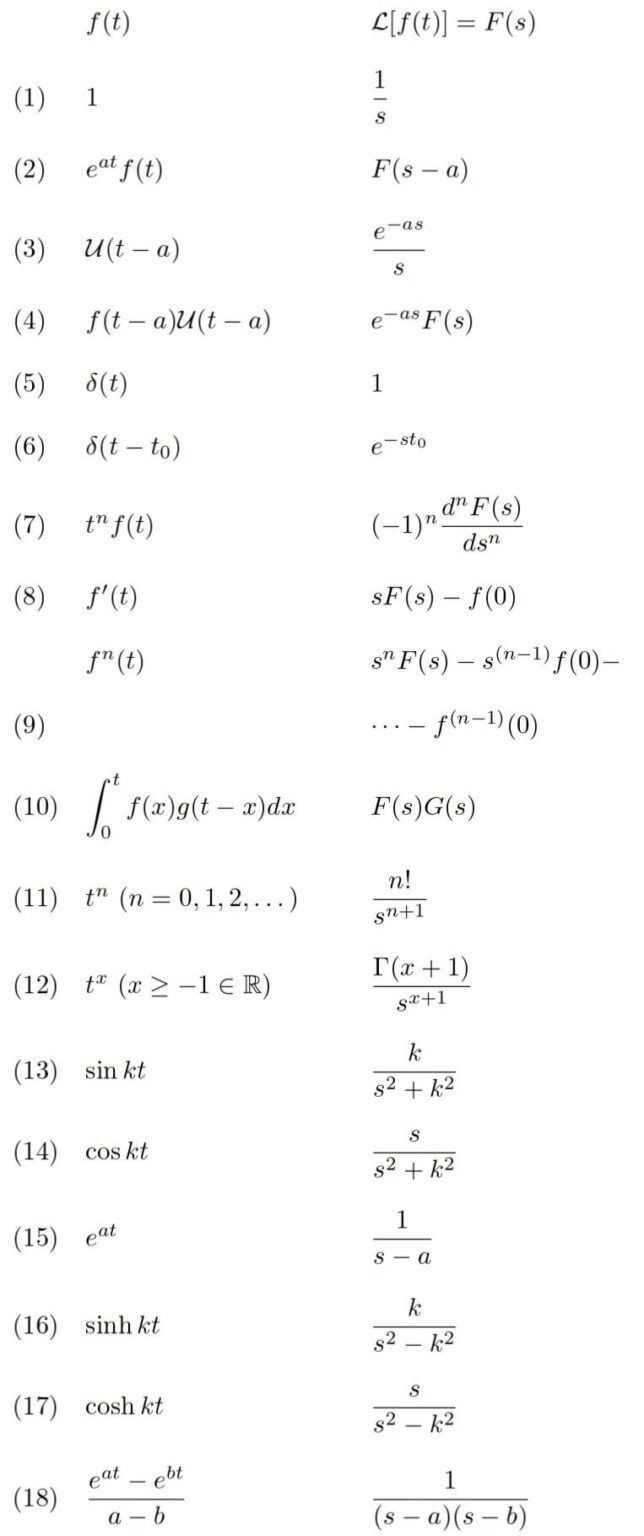
Using the calculator is straightforward. Follow these steps:
- Input the Function: Enter the Laplace domain function into the calculator.
- Select the Method: Choose the appropriate method for the transformation (e.g., partial fractions, convolution theorem).
- Compute the Result: Click the calculate button to get the time-domain function.
✨ Note: Ensure the input function is in the correct format to avoid errors.
Example Calculation
Consider the Laplace domain function ( F(s) = \frac{2s + 1}{s^2 + 4s + 5} ). Using the calculator, you can instantly find its inverse Laplace transform, ( f(t) ), without tedious manual work.
Benefits of Online Inverse Laplace Transform Calculators
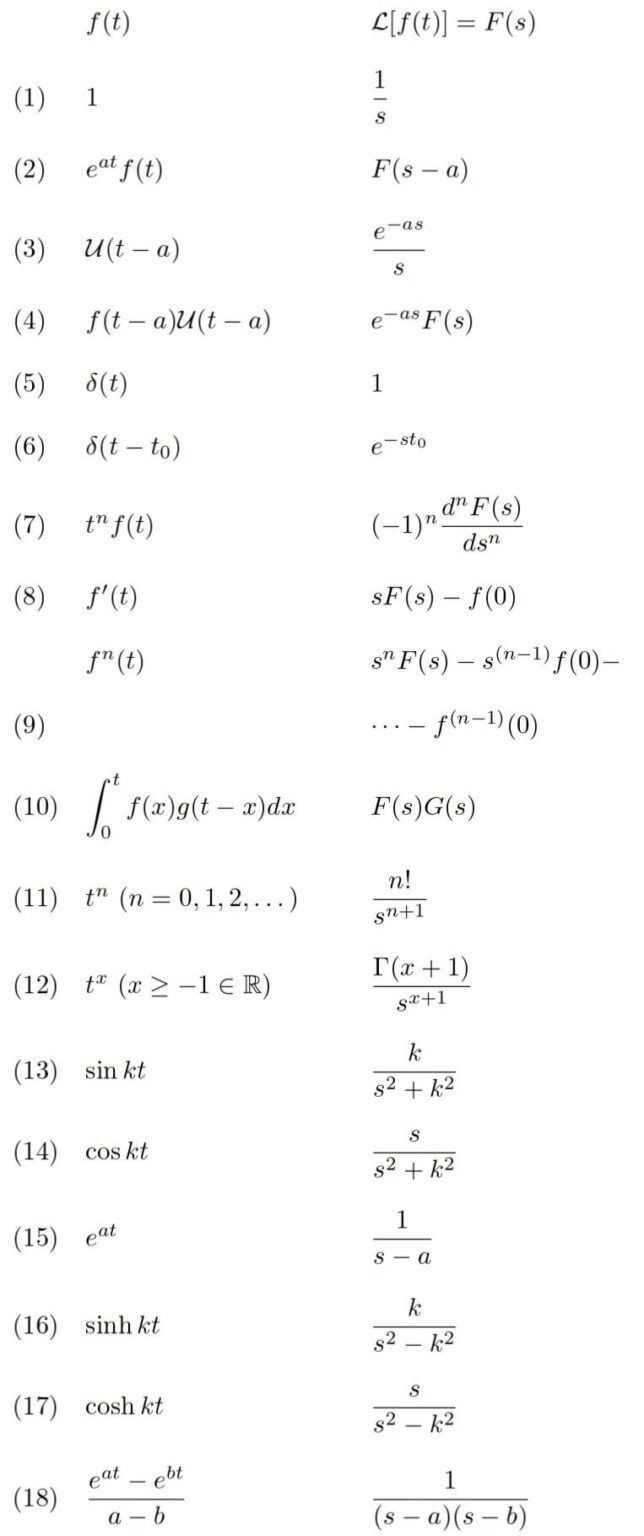
Online calculators offer additional perks:
- User-Friendly Interface: Intuitive design for easy navigation.
- Step-by-Step Solutions: Some tools provide detailed steps for better understanding.
- Free Access: Many calculators are available at no cost.
Applications of Inverse Laplace Transform
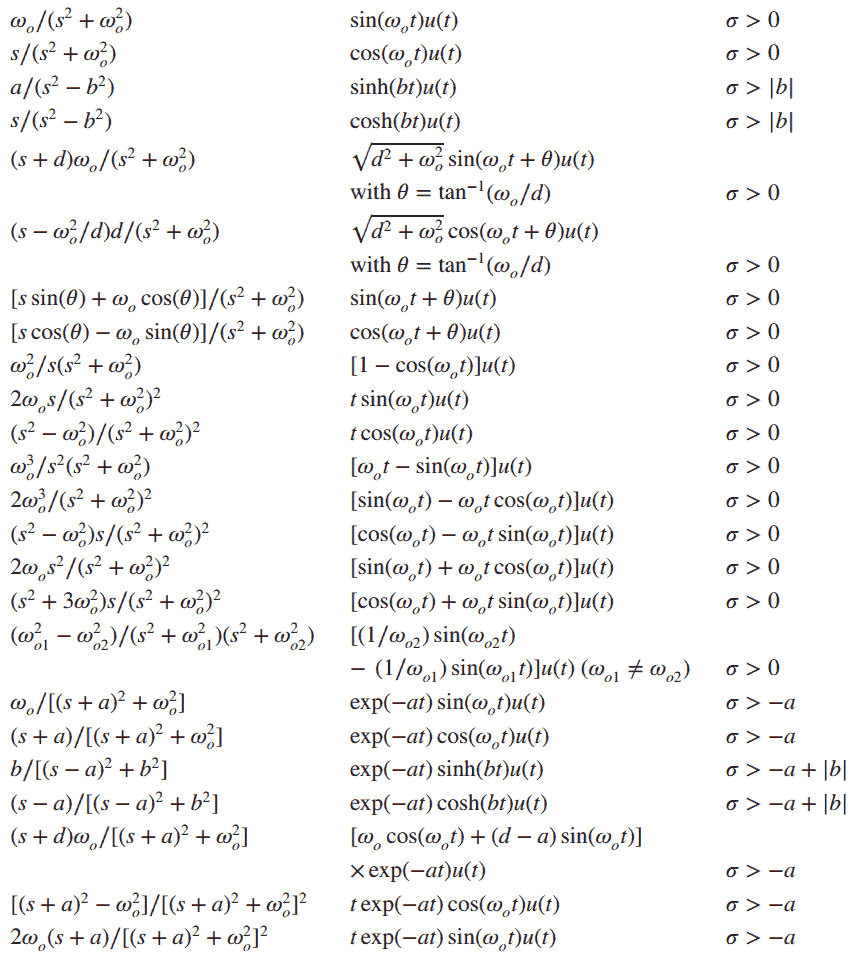
The Inverse Laplace Transform is widely used in:
- Control Systems: Analyzing system responses.
- Circuit Theory: Solving RLC circuits.
- Signal Processing: Transforming frequency-domain signals to time-domain.
Choosing the Right Calculator
When selecting an Inverse Laplace Transform Calculator, consider:
- Accuracy: Ensure the tool provides precise results.
- Features: Look for additional functionalities like graphing or step-by-step solutions.
- Reviews: Check user feedback for reliability.
| Feature | Importance |
|---|---|
| Accuracy | High |
| Ease of Use | Medium |
| Additional Tools | Low |
Final Thoughts
An Inverse Laplace Transform Calculator is an indispensable tool for anyone dealing with complex mathematical functions. It simplifies calculations, saves time, and enhances accuracy. Whether you’re a student or a professional, incorporating this tool into your workflow can significantly improve your productivity.
What is the Inverse Laplace Transform?
+The Inverse Laplace Transform is a mathematical operation that converts a function from the Laplace domain back to the time domain.
Can I use the calculator for any function?
+Most calculators support a wide range of functions, but complex or unconventional functions may require specific tools.
Are online calculators accurate?
+Reputable online calculators are highly accurate, but always double-check results for critical applications.
Laplace Transform Calculator, Inverse Laplace Transform Applications, Online Mathematical Tools
