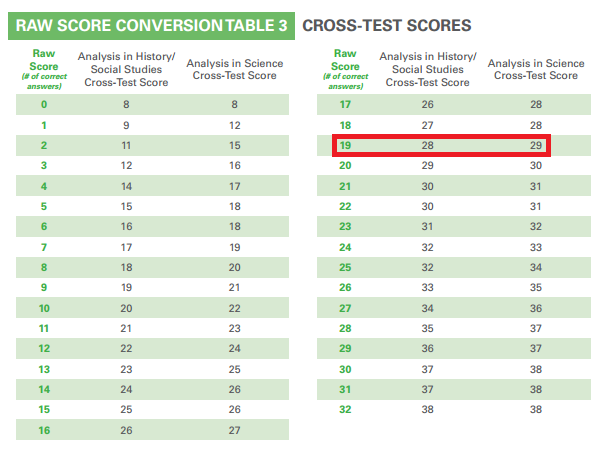
Understanding the Inverse of Exponential Functions: A Quick Guide
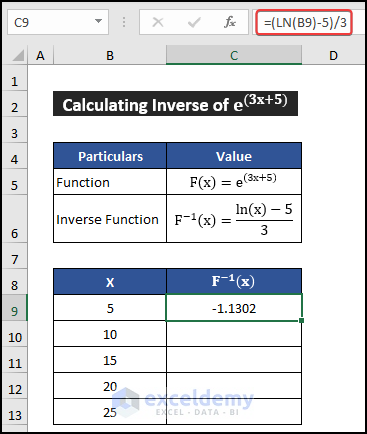
Understanding the inverse of exponential functions is crucial for anyone diving into advanced mathematics or applying these concepts in real-world scenarios. Whether you're a student, a data analyst, or a curious learner, grasping this topic unlocks a deeper understanding of growth and decay patterns. In this guide, we'll break down the concept step-by-step, ensuring clarity and practicality. From defining exponential functions to deriving their inverses, we’ve got you covered. Let’s explore how to master this essential mathematical tool, exponential functions, inverse functions, mathematical concepts.
What Are Exponential Functions?

Exponential functions are mathematical expressions of the form ( f(x) = a^x ), where ( a ) is a positive constant called the base. These functions model rapid growth or decay, making them vital in fields like finance, biology, and physics. For instance, compound interest and population growth are classic examples of exponential behavior. Understanding their properties is the first step toward mastering their inverses, exponential growth, compound interest, mathematical modeling.
The Inverse of Exponential Functions
The inverse of an exponential function is a logarithmic function. Specifically, if ( f(x) = a^x ), its inverse is ( f^{-1}(x) = \log_a(x) ). This relationship is fundamental in solving equations involving exponentials and logarithms. By finding the inverse, you can “undo” the exponential operation, making it easier to solve for unknowns in complex problems, logarithmic functions, solving equations, mathematical inverses.
Deriving the Inverse
To derive the inverse of ( f(x) = a^x ):
1. Start with ( y = a^x ).
2. Swap ( x ) and ( y ): ( x = a^y ).
3. Solve for ( y ): ( y = \log_a(x) ).
This process highlights the intrinsic link between exponentials and logarithms, deriving inverses, logarithmic properties, mathematical derivations.
📌 Note: Always ensure the base a is positive and not equal to 1 for exponential and logarithmic functions to be well-defined.
Practical Applications
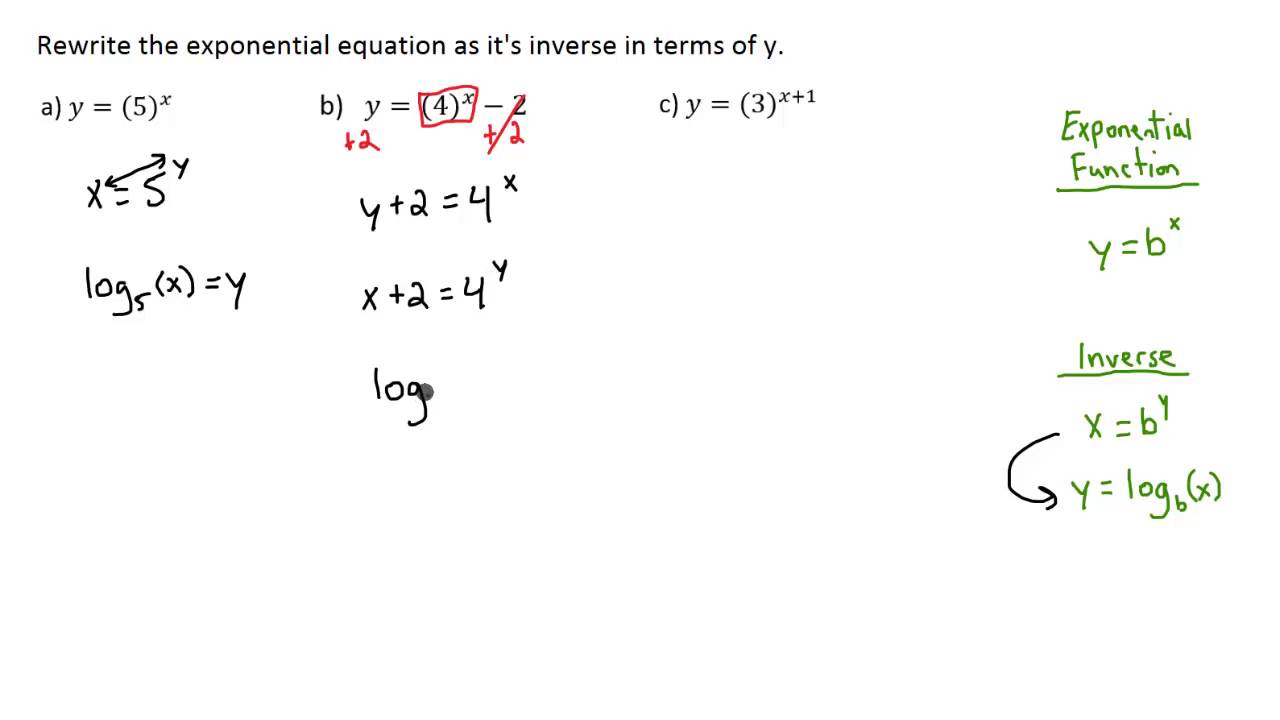
The inverse of exponential functions isn’t just theoretical—it’s applied in numerous real-world scenarios:
- Finance: Calculating loan payments or investment growth.
- Science: Modeling decay rates in radioactive substances.
- Technology: Analyzing algorithmic complexity in computer science.
Mastering this concept empowers you to tackle complex problems with confidence, financial modeling, scientific applications, technological analysis.
Checklist: Mastering the Inverse of Exponential Functions
- Understand the definition of exponential functions.
- Learn the relationship between exponentials and logarithms.
- Practice deriving inverses step-by-step.
- Apply concepts to real-world problems.
- Use tools like graphing calculators or software for visualization.
What is the inverse of an exponential function?
+The inverse of an exponential function f(x) = a^x is a logarithmic function f^{-1}(x) = \log_a(x) .
Why are exponential and logarithmic functions inverses?
+They are inverses because one "undoes" the operation of the other. Exponentials raise a base to a power, while logarithms determine the exponent needed to achieve a given value.
Where are inverses of exponential functions used?
+They are used in finance, science, technology, and more, to solve problems involving growth, decay, and complex equations.
By now, you should have a solid grasp of the inverse of exponential functions and their applications. From deriving inverses to solving real-world problems, this knowledge is a powerful tool in your mathematical arsenal. Keep practicing, and soon you’ll tackle even the most challenging equations with ease. Happy learning, mathematical mastery, problem-solving skills, exponential and logarithmic functions!