Understanding the Mean Value Integral Theorem: Key Insights

The Mean Value Theorem (MVT) is a cornerstone in calculus, offering profound insights into the behavior of continuous and differentiable functions. By understanding this theorem, you unlock a deeper comprehension of how functions change over intervals, making it an essential tool for mathematicians, engineers, and scientists alike. Whether you’re solving complex problems or simply curious about the intricacies of calculus, the Mean Value Theorem provides a bridge between a function’s average rate of change and its instantaneous rate of change. Let’s dive into the key insights and applications of this fundamental theorem, ensuring you grasp its significance in both theoretical and practical contexts. (Mean Value Theorem, Calculus Insights, Function Analysis)

What is the Mean Value Theorem?

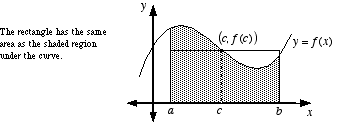
The Mean Value Theorem states that if a function ( f ) is continuous on the closed interval ([a, b]) and differentiable on the open interval ((a, b)), then there exists at least one point ( c ) in ((a, b)) such that:

[ f’© = \frac{f(b) - f(a)}{b - a} ]

In simpler terms, the theorem guarantees that the slope of the secant line connecting the endpoints of the interval is equal to the derivative of the function at some point within the interval. This theorem is a powerful tool for understanding the relationship between a function’s average rate of change and its instantaneous rate of change. (Mean Value Theorem, Calculus Fundamentals, Derivative Applications)

Key Insights into the Mean Value Theorem

1. Guarantees a Point of Equality

The Mean Value Theorem ensures that there is at least one point ( c ) where the derivative equals the average rate of change. This insight is crucial for analyzing function behavior and proving other theorems in calculus. (Function Behavior, Derivative Analysis, Calculus Proofs)

2. Implies Constant Functions

If ( f’(x) = 0 ) for all ( x ) in ((a, b)), the theorem implies that ( f(x) ) is constant on ([a, b]). This is a direct consequence of the theorem and highlights its utility in identifying constant functions. (Constant Functions, Derivative Properties, Calculus Insights)

3. Applications in Real-World Problems

The Mean Value Theorem is applied in various fields, from physics to economics, to model rates of change and optimize functions. For instance, it can be used to determine if a moving object achieves a certain speed within a given time interval. (Real-World Applications, Optimization, Physics and Calculus)

📌 Note: The Mean Value Theorem assumes the function is continuous and differentiable, so always verify these conditions before applying it.

Practical Steps to Apply the Mean Value Theorem

To apply the Mean Value Theorem effectively, follow these steps:

1. Verify Continuity and Differentiability: Ensure the function is continuous on ([a, b]) and differentiable on ((a, b)).
   
2. Calculate the Average Rate of Change: Compute (\frac{f(b) - f(a)}{b - a}).
   
3. Find the Derivative: Determine ( f’(x) ).
   
4. Set Up the Equation: Solve ( f’© = \frac{f(b) - f(a)}{b - a} ) for ( c ).
   

📌 Note: The theorem guarantees at least one c , but there may be multiple solutions depending on the function.

Checklist for Mastering the Mean Value Theorem

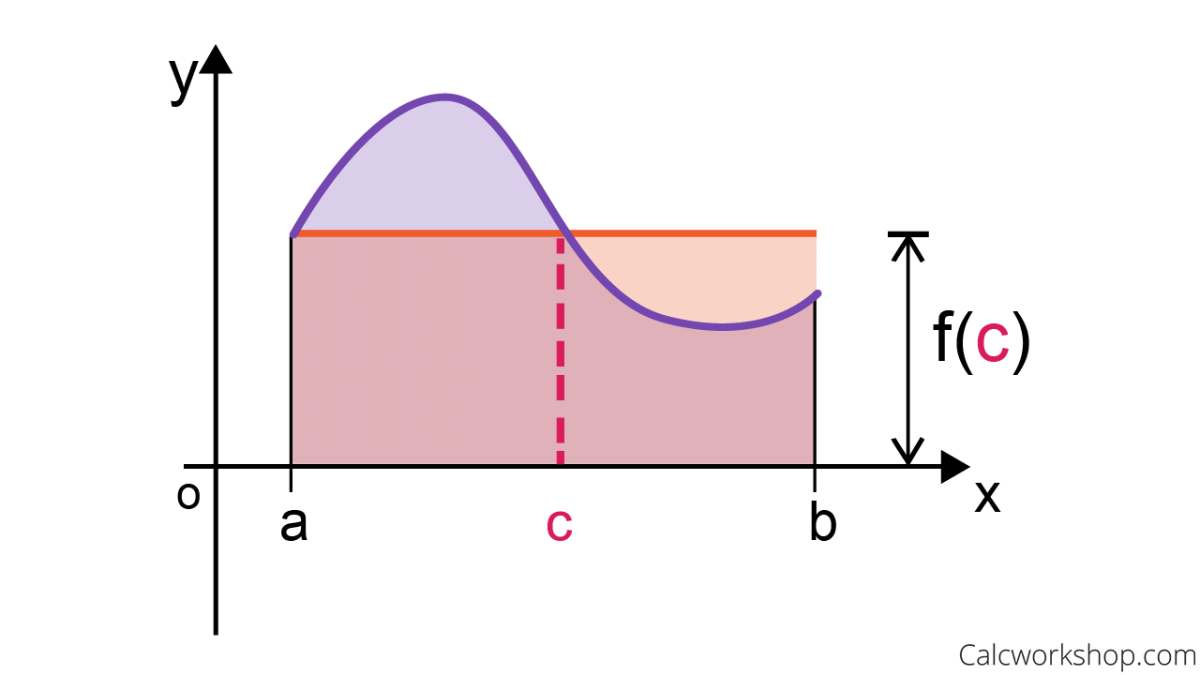
• [ ] Understand the conditions: continuity on ([a, b]) and differentiability on ((a, b)).
  
• [ ] Practice calculating average rates of change.
  
• [ ] Solve for ( c ) using the derivative and average rate of change.
  
• [ ] Apply the theorem to real-world scenarios.
  

To wrap up, the Mean Value Theorem is a fundamental concept in calculus that bridges the gap between average and instantaneous rates of change. By mastering this theorem, you gain a powerful tool for analyzing functions and solving complex problems. Whether you’re a student, educator, or professional, understanding the Mean Value Theorem enhances your mathematical toolkit and opens doors to advanced applications in science and engineering. (Calculus Mastery, Mathematical Tools, Advanced Applications)