Understanding the concepts of mutually exclusive and independent events is crucial in probability theory and statistics. These terms often appear in academic discussions, data analysis, and real-world applications. While they might seem similar, they describe fundamentally different relationships between events. This blog post will break down their definitions, key differences, and practical examples to help you grasp these concepts effectively.
What Are Mutually Exclusive Events?
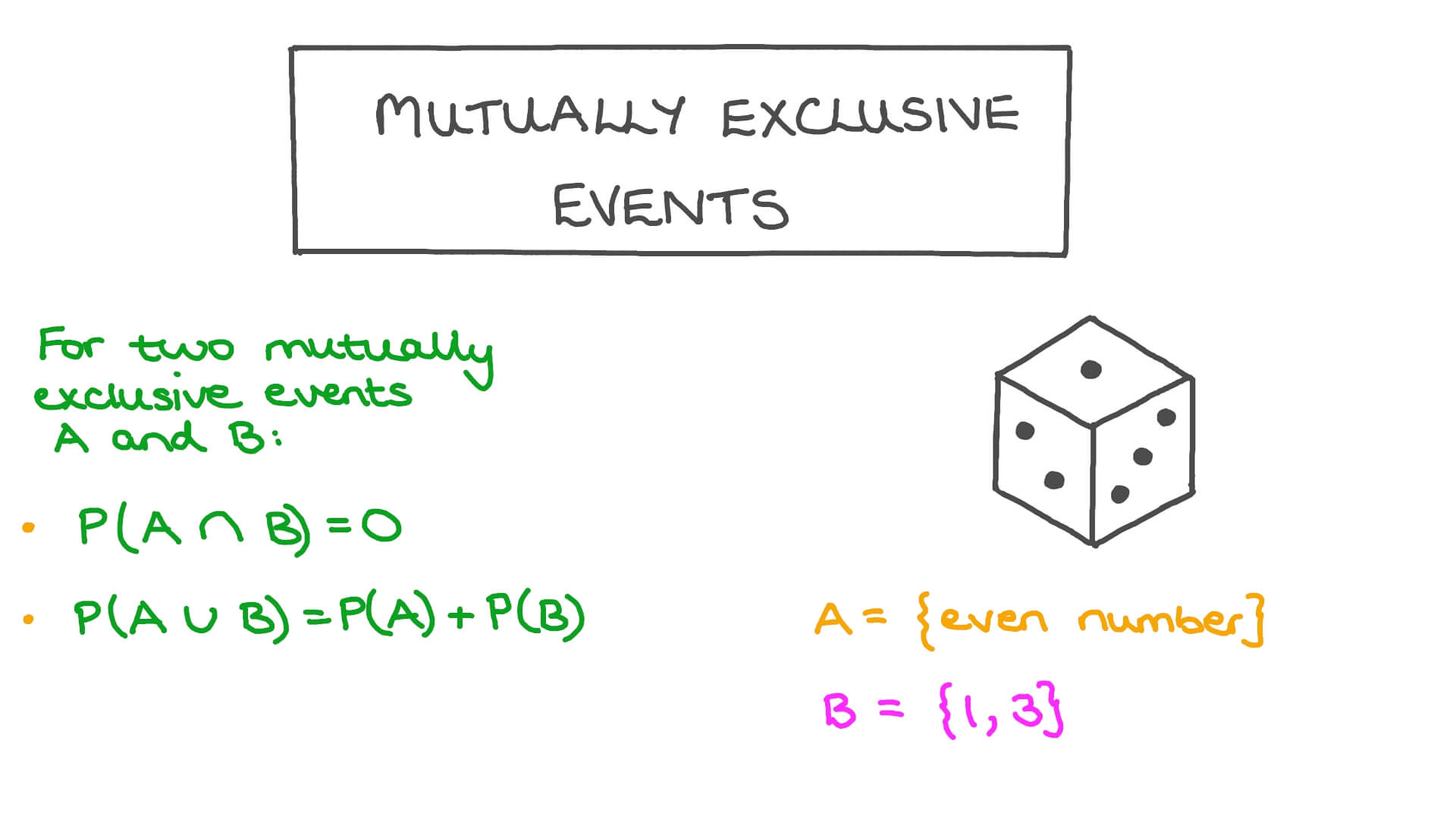
Mutually exclusive events are events that cannot occur at the same time. If one event happens, the other cannot. For example, flipping a coin results in either heads or tails, but not both.
- Key Characteristics:
- Cannot coexist: If Event A occurs, Event B cannot.
- Probability Rule: ( P(A \text{ and } B) = 0 ).
- Cannot coexist: If Event A occurs, Event B cannot.
💡 Note: Mutually exclusive events are often visualized as distinct categories with no overlap.
What Are Independent Events?
Independent events are events where the occurrence of one does not affect the probability of the other. For instance, flipping a coin twice: the outcome of the first flip does not influence the second.
- Key Characteristics:
- No influence: The probability of one event remains unchanged by the other.
- Probability Rule: ( P(A \text{ and } B) = P(A) \times P(B) ).
- No influence: The probability of one event remains unchanged by the other.
Key Differences Between Mutually Exclusive and Independent Events
| Aspect | Mutually Exclusive | Independent |
|---|---|---|
| Occurrence | Cannot happen together. | Can happen together. |
| Probability Rule | ( P(A \text{ and } B) = 0 ) | ( P(A \text{ and } B) = P(A) \times P(B) ) |
| Example | Rolling a 2 and a 3 on a single die. | Rolling a die and flipping a coin. |
Practical Examples to Clarify Concepts
Mutually Exclusive Example
Imagine a weather forecast predicting either rain or sunshine on a given day. If it rains, it cannot be sunny, and vice versa.
Independent Example
Consider two separate coin flips. The outcome of the first flip (heads or tails) does not affect the outcome of the second flip.
Checklist: Identifying Mutually Exclusive vs Independent Events
Mutually Exclusive:
- Can both events occur simultaneously? If no, they are mutually exclusive.
- Check if ( P(A \text{ and } B) = 0 ).
- Can both events occur simultaneously? If no, they are mutually exclusive.
Independent:
- Does the occurrence of one event affect the probability of the other? If no, they are independent.
- Verify if ( P(A \text{ and } B) = P(A) \times P(B) ).
- Does the occurrence of one event affect the probability of the other? If no, they are independent.
In summary, mutually exclusive events cannot happen together, while independent events do not influence each other’s probabilities. Understanding these distinctions is essential for accurate probability calculations and real-world applications.
Can two events be both mutually exclusive and independent?
+No, mutually exclusive events cannot be independent because if one occurs, the other cannot, violating the independence condition.
How do I determine if events are mutually exclusive or independent?
+Use the probability rules: P(A \text{ and } B) = 0 for mutually exclusive, and P(A \text{ and } B) = P(A) \times P(B) for independent events.
What is an example of events that are neither mutually exclusive nor independent?
+Drawing cards from a deck without replacement: the events are dependent and can overlap (e.g., drawing a heart and a red card).
probability theory,statistics,data analysis,mutually exclusive events,independent events
