Mastering Parametric Differentiation: Second Derivative Explained
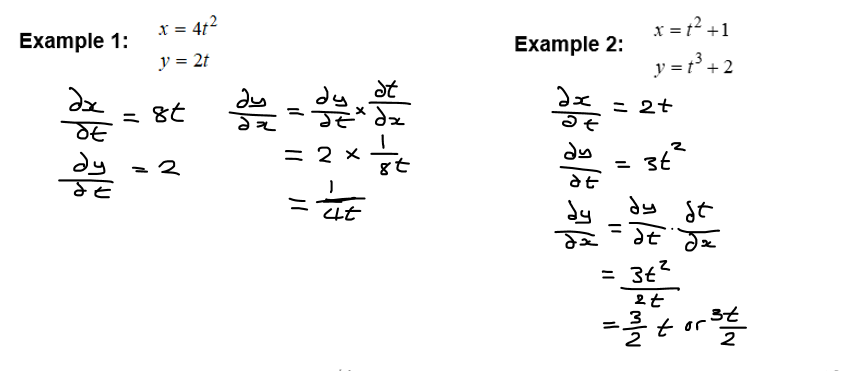
Mastering parametric differentiation is essential for anyone diving into calculus, especially when dealing with the second derivative. Whether you're a student, researcher, or professional, understanding how to compute and interpret second derivatives in parametric equations can unlock deeper insights into curve behavior, concavity, and optimization. This guide breaks down the process step-by-step, ensuring you grasp both the theory and practical applications. From foundational concepts to advanced techniques, we’ll cover everything you need to know to master this critical skill. (parametric equations, second derivative, calculus)
What is Parametric Differentiation?

Parametric differentiation involves expressing coordinates ( x ) and ( y ) as functions of a parameter ( t ). Instead of ( y = f(x) ), we have ( x = f(t) ) and ( y = g(t) ). The first derivative ( \frac{dy}{dx} ) is found using the chain rule:
[
\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}
]
The second derivative builds on this by differentiating ( \frac{dy}{dx} ) again with respect to ( t ). (chain rule, first derivative, parametric equations)
How to Compute the Second Derivative in Parametric Form

To find the second derivative ( \frac{d^2y}{dx^2} ), follow these steps:
- Step 1: Compute ( \frac{dy}{dt} ) and ( \frac{dx}{dt} ).
- Step 2: Find the first derivative ( \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ).
- Step 3: Differentiate ( \frac{dy}{dx} ) with respect to ( t ) using the quotient rule or chain rule.
- Step 4: Substitute into the formula:
[
\frac{d^2y}{dx^2} = \frac{\frac{d}{dt}\left(\frac{dy}{dx}\right)}{\frac{dx}{dt}}
]
📘 Note: Ensure ( \frac{dx}{dt} \neq 0 ) to avoid division by zero. (quotient rule, chain rule, second derivative)
Applications of the Second Derivative in Parametric Equations

The second derivative reveals crucial information about parametric curves:
- Concavity: Determines if the curve is concave up (( \frac{d^2y}{dx^2} > 0 )) or concave down (( \frac{d^2y}{dx^2} < 0 )).
- Points of Inflection: Identifies where concavity changes (( \frac{d^2y}{dx^2} = 0 )).
- Optimization: Used in finding maximum or minimum values of parametric functions. (concavity, inflection points, optimization)
Example: Finding the Second Derivative

Consider the parametric equations ( x = t^2 ) and ( y = t^3 ). Let’s compute the second derivative:
| Step | Calculation |
|---|---|
| 1 | ( \frac{dx}{dt} = 2t ), ( \frac{dy}{dt} = 3t^2 ) |
| 2 | ( \frac{dy}{dx} = \frac{3t^2}{2t} = \frac{3t}{2} ) |
| 3 | ( \frac{d}{dt}\left(\frac{3t}{2}\right) = \frac{3}{2} ) |
| 4 | ( \frac{d^2y}{dx^2} = \frac{\frac{3}{2}}{2t} = \frac{3}{4t} ) |

📘 Note: This example assumes ( t \neq 0 ). (parametric equations, second derivative, example)
Checklist for Mastering Parametric Second Derivatives

- Understand the chain rule and quotient rule.
- Compute ( \frac{dx}{dt} ) and ( \frac{dy}{dt} ) first.
- Differentiate ( \frac{dy}{dx} ) with respect to ( t ).
- Apply the second derivative formula correctly.
- Analyze concavity and inflection points using the result. (checklist, second derivative, concavity)
Mastering the second derivative in parametric differentiation is a powerful skill that enhances your ability to analyze curves and solve complex problems. By following the steps outlined in this guide, you’ll gain confidence in handling parametric equations and their derivatives. Practice with various examples to solidify your understanding and explore advanced applications in fields like physics, engineering, and economics. (parametric differentiation, second derivative, calculus)
What is parametric differentiation?
+
Parametric differentiation involves finding derivatives of ( x ) and ( y ) with respect to a parameter ( t ), often used when ( x ) and ( y ) are defined as functions of ( t ).
Why is the second derivative important in parametric equations?
+
The second derivative helps determine concavity, inflection points, and optimization in parametric curves, providing deeper insights into their behavior.
How do I avoid division by zero in parametric differentiation?
+
Ensure ( \frac{dx}{dt} \neq 0 ) when computing ( \frac{dy}{dx} ) and its derivatives to avoid undefined results.