Mastering the Root Mean Square Formula: A Quick Guide

<!DOCTYPE html>
Understanding the Root Mean Square (RMS) formula is essential for anyone working with electrical systems, signal processing, or data analysis. Whether you're an engineer, student, or enthusiast, mastering this concept can significantly enhance your problem-solving skills. In this guide, we’ll break down the RMS formula, its applications, and how to calculate it step-by-step. By the end, you’ll have a clear understanding of RMS and its practical uses. (Root Mean Square Formula, Electrical Engineering, Signal Processing)
What is the Root Mean Square (RMS) Formula?

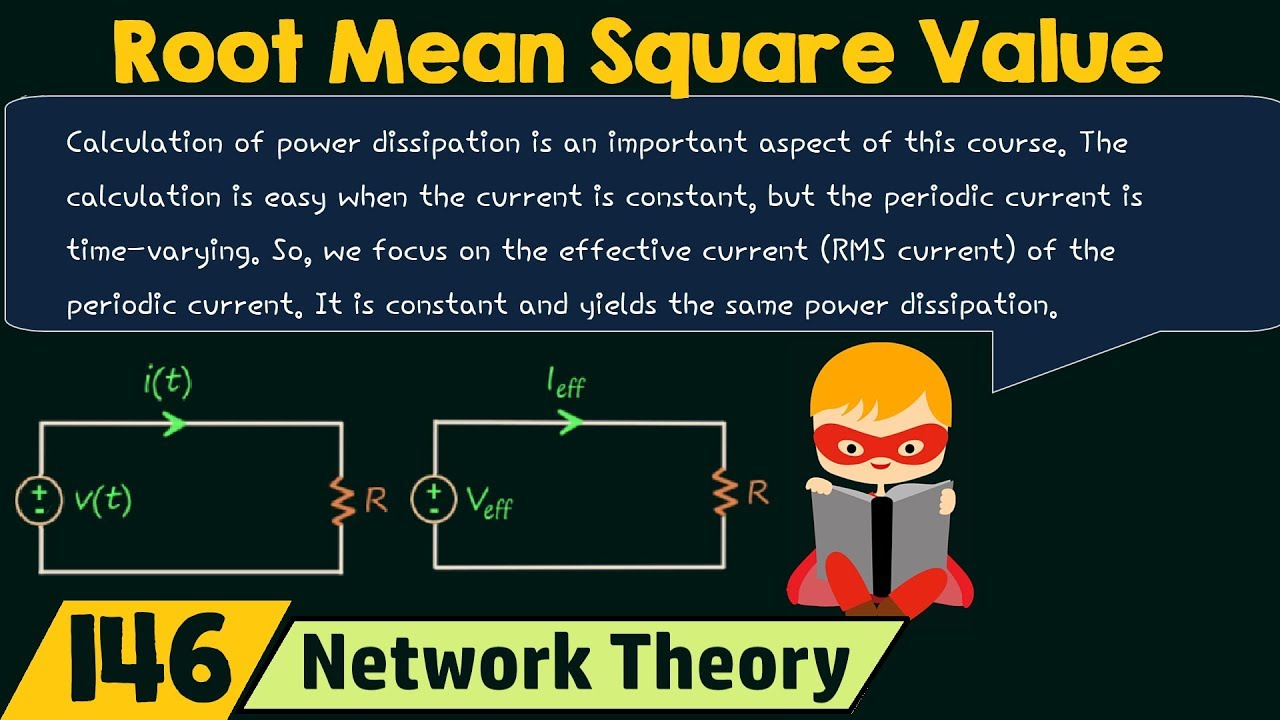
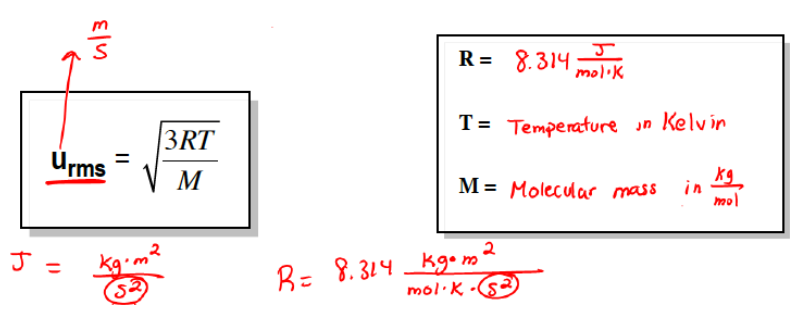
The Root Mean Square (RMS) is a statistical measure that calculates the effective value of a varying quantity, such as voltage or current in AC circuits. It represents the equivalent steady DC value that produces the same heating effect or power dissipation. The RMS formula is given by:
RMS = √(∑(xi2) / n)
Where:
- xi = individual values in the dataset
- n = total number of values
💡 Note: RMS is widely used in electrical engineering to determine the heating effect of AC currents and voltages. (RMS Calculation, AC Circuits, Power Dissipation)
Step-by-Step Guide to Calculating RMS

Step 1: Square Each Value
Start by squaring each value in your dataset. For example, if your dataset is [1, 2, 3, 4], the squared values will be [1, 4, 9, 16]. (Data Analysis, Mathematical Steps)
Step 2: Calculate the Mean of Squared Values
Sum the squared values and divide by the total number of values. Using the example above: (1 + 4 + 9 + 16) / 4 = 7.5. (Mean Calculation, Statistical Measures)
Step 3: Take the Square Root
Finally, take the square root of the mean calculated in Step 2. For our example, √7.5 ≈ 2.74. This is the RMS value. (Square Root Operation, Final Calculation)
Practical Applications of RMS
The RMS formula has numerous applications across different fields:
| Field | Application |
|---|---|
| Electrical Engineering | Calculating AC voltage and current for power dissipation. |
| Signal Processing | Measuring the amplitude of varying signals. |
| Data Analysis | Analyzing the magnitude of fluctuating data. |
📌 Note: RMS is particularly useful in scenarios where the average value alone doesn’t provide sufficient information. (Practical Applications, Real-World Uses)
Checklist for Mastering RMS

- Understand the RMS formula and its components.
- Practice calculating RMS with sample datasets.
- Apply RMS in real-world scenarios like AC circuit analysis.
- Use tools or software for quick RMS calculations when needed.
Mastering the Root Mean Square (RMS) formula opens up a world of possibilities in engineering, data analysis, and beyond. By following this quick guide, you’ll be well-equipped to apply RMS in various practical situations. Remember, practice makes perfect—so keep calculating and exploring its applications. (Mastering RMS, Practical Guide, Engineering Tools)
What is the difference between RMS and average value?
+The RMS value considers the magnitude of values by squaring them before averaging, making it more suitable for measuring the effective value of varying quantities. The average value simply sums the values and divides by the count. (RMS vs Average, Value Comparison)
Why is RMS important in electrical engineering?
+RMS is crucial in electrical engineering because it determines the heating effect of AC currents and voltages, which is essential for designing safe and efficient electrical systems. (Electrical Engineering Importance, AC Systems)
Can RMS be used for non-electrical applications?
+Yes, RMS is used in signal processing, data analysis, and other fields to measure the magnitude of fluctuating values. (Non-Electrical Applications, Versatile Uses)