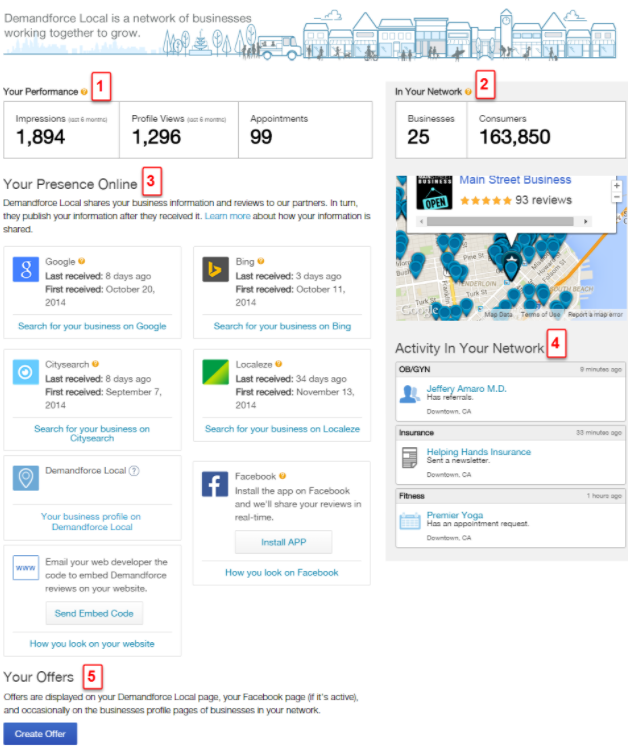
<!DOCTYPE html>
Understanding the second derivative of parametric equations is crucial for analyzing the curvature and concavity of curves. Whether you’re a student, researcher, or professional, mastering this concept can enhance your problem-solving skills in calculus and physics. This guide breaks down the process into simple steps, ensuring clarity and practicality.
What Are Parametric Equations?
Parametric equations define the coordinates of points on a curve as functions of a parameter, usually denoted as ( t ). For example, ( x = f(t) ) and ( y = g(t) ) describe a curve in the Cartesian plane. These equations are widely used in modeling motion, engineering, and computer graphics. (parametric equations,calculus fundamentals)
First Derivative of Parametric Equations
The first derivative ( \frac{dy}{dx} ) is found using the chain rule: [ \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ]. This derivative represents the slope of the tangent line to the curve at any point. (first derivative,chain rule)
Second Derivative of Parametric Equations
The second derivative ( \frac{d^2y}{dx^2} ) measures the rate of change of the slope and is calculated as: [ \frac{d^2y}{dx^2} = \frac{\frac{d}{dt}\left(\frac{dy}{dx}\right)}{\frac{dx}{dt}} ]. This helps determine concavity and inflection points. (second derivative,concavity analysis)
Step-by-Step Calculation
- Step 1: Compute ( \frac{dx}{dt} ) and ( \frac{dy}{dt} ).
- Step 2: Find ( \frac{dy}{dx} ) using the formula ( \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ).
- Step 3: Differentiate ( \frac{dy}{dx} ) with respect to ( t ).
- Step 4: Divide the result by ( \frac{dx}{dt} ) to obtain ( \frac{d^2y}{dx^2} ).
📘 Note: Ensure ( \frac{dx}{dt} \neq 0 ) to avoid division by zero errors.
Applications of Second Derivatives
The second derivative is essential for:
- Determining curve concavity.
- Finding inflection points.
- Analyzing motion in physics.
Checklist for Calculating Second Derivatives
- Verify parametric equations ( x = f(t) ) and ( y = g(t) ).
- Compute ( \frac{dx}{dt} ) and ( \frac{dy}{dt} ).
- Find ( \frac{dy}{dx} ) using the chain rule.
- Differentiate ( \frac{dy}{dx} ) with respect to ( t ).
- Divide by ( \frac{dx}{dt} ) to get ( \frac{d^2y}{dx^2} ).
Mastering the second derivative of parametric equations opens doors to advanced mathematical and scientific applications. By following this simplified guide, you’ll gain confidence in tackling complex problems efficiently. (advanced calculus,mathematical applications)
What are parametric equations used for?
+Parametric equations are used to describe curves and trajectories in calculus, physics, and engineering, especially when the relationship between ( x ) and ( y ) is complex.
How do I find the first derivative of parametric equations?
+Use the formula ( \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ), applying the chain rule.
Why is the second derivative important?
+The second derivative helps determine the concavity of a curve and identifies inflection points, which are crucial for understanding the curve’s shape.
